Holbein’s Sketch of the Holy Family with St. Anne and St. Joachim (1518-19)

Holbein’s sketch of the Holy Family with two saints therefore offers a striking advance from the stolid one-point perspectives of the early Renaissance. It is staged in an unabashed oblique view, with the drama of the eye level at the foot of the tableau. Rather than the plain archways of prior work, Holbein develops a complex structure of receding vaults and chamfers. To do so requires an understanding of the projection of the semi-circular structures in the portico to oblique ellipses in the plane of the picture. This is a challenging geometrical construction, especially in the early 1500s. Even now, few artists would know how to generate the nested ellipses in the right configuration to match the intended structure.

In view of the timing of Holbein’s work, it is interesting that Jean Pélérin (the ‘’Viator’) had recently published an analysis of the two-point construction in 1505. He was French, and published in Toul, a town in the Lorraine district northwest of Switzerland. The book was pirated in an illustrated edition Nuremberg, again just north of Switzerland, in 1509. It is thus highly plausible that a copy was available to Holbein in Basle at that time. His friend, Nicolas Copernicus, had lived in the same area, moving from Padua to to Frauenburg, in 1512 and published his ‘De Revolutionibus’ in Nuremberg in 1543.

Detailed analysis of the archway in this sketch leads to the conclusion that Holbein used a sophisticated construction method for the elliptical curves and the converging details, with a few minor conceptual lapses. The lapses are interesting because they indicate that he must have employed a geometric construction of some kind rather than an optical projection method, such as a camera obscura. Use of an optical projection method might have resulted in inaccuracies of transcription as he traced the image onto the paper, but it would not have generated conceptual errors in the construction logic.

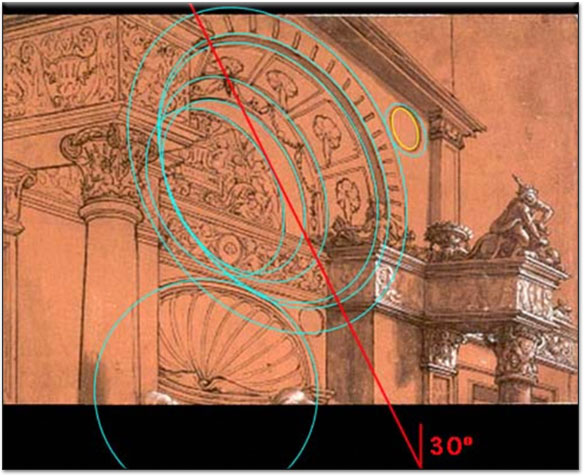
Fig. 1. Elliptical construction of the portico

Holbein’s construction is sophisticated because the primary construction of the portico contains a set of six nested circles, which project to ellipses in the oblique view that Holbein chose for this sketch. At this point in history, it is not clear whether artists appreciated the rule that circular structures always project to ellipses in oblique view. The mathematical proof is difficult and the result counterintuitive. Up until this time, artists had mostly restricted themselves to circular arches shown frontal to the canvas, or non-circular arches. Where oblique arches are shown, they usually are in a narrow angle of projection where the details of the ellipse are hard to discern. It is interesting, therefore, to attempt to identify the first use of accurately elliptical construction.

Nevertheless, the construction analysis for this sketch makes clear that Holbein’s curves are essentially perfect ellipses. For each curve of the portico, an ellipse can be found that follows almost perfectly the curve that he has drawn. It seems, then, that he must have been aware of the fact that circles project to ellipses, and also have had access to some method of drawing ellipses where he wished to place them. Not only this, but the method must have allowed flexible control of the ellipse placement, because his ellipses are all at exactly the same angle (30º in this case) and are nested a fashion appropriate to the spatial relationships of the circular arcs from which they derive. The angle of view is such that the lower left edges of the contours within the funnel-shaped portico all coincide. The outer circle, however, shows an expansion in the plane of the wall. For this reason it is larger at all points than the next circle for the inner rim of the coping, and hence the lower edges of the two outer circles do not coincide. Finally, there is a tubular section leading to the inmost curve, so again the lower edges should not coincide.

Another place where the construction is demanding is in the scallop shell fountain below the portico. Here the actual shape of the shell alcove is a flattened ellipse; at least, that is how we perceive it when viewing the sketch. The perspective foreshortening squeezes this ellipse and, by the inverse geometrical theorem, returns it to a circular shape on the page. Apparently Holbein was aware of this inverse property because the outline of the shell forms an almost perfect circular arc.
Holbein has captured the elliptical projection of all these properties essentially perfectly. These days, such a construction could be readily achieved by use of a sheet of ellipse templates, but it is far from obvious what method Holbein could have used to generate such a precise alignment. The only place where he deviates from the required construction is in the two small circles at the corners of the structure. The enclosing turquoise ellipse shows the required orientation of the projection, at 30º to match the orientation of the other ellipses. But it is very clear Holbein must have drawn this small ellipse by hand, since it is quite wobbly. Moreover, the yellow ellipse indicates the best-fitting orientation, which is at 20º rather than 30º. The mismatch is fairly noticeable in the original.