Fig.7.12 Drawing of cube indicating angles comprising fork juncture and arrow juncture.

Thus we are led to the alternative to semantics: that an angle in a picture is seen as a representation of a right angle only when it is perceived as a part of a representation of a rectangular corner. To understand how this can be done, we must consider junctures, the local features that represent the vertices of objects that have straight edges. Figure 7.12 is the drawing of a cube in which two of the junctures have been labeled, for obvious reasons, fork and arrow junctures. Perkins (1968, 1972, 1973) formulated the following laws: Perkins's first law. A fork juncture is perceived as the vertex of a cube if and only if the measure of each of the three angles is greater than 90°. Perkins's second law. An arrow juncture is perceived as the vertex of a cube if and only if the measure of each of the two angles is less than 90° and the sum of their measures is greater than 90°.

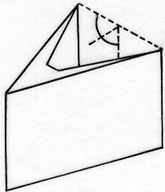
Figure 7.10 obeys Perkins's laws, whereas the form in Figure 7.13 does not; the former looks rectangular, the latter does not. Perkins's laws can be extended to junctures that are not themselves rectangular, but that are part of bodies that can be decomposed into two congruent bodies, each of which has a rectangular juncture. Figure 7.14 shows an object that is seen as a rectangular prism with a mirror symmetric irregular pentagonal cross section. We have added auxiliary lines to the drawing to indicate the plane of symmetry and a line joining two symmetric vertices of the cross section. The arrow juncture obtained in the process of drawing these auxiliary lines satisfies Perkins's second law and is therefore seen as the vertex of a cube, which implies the other perceived features. Figure 7.15, on the other hand, does not look symmetric, and there is some question regarding whether its upper surface looks orthogonal to the sides.

		Fig.7.13 Drawing of three-dimensional object that does not look rectangular and does not obey Perkins's laws.

These laws, with their emphases on 90° angles in the picture, are related to a special case of central projection, in which the center of projection is infinitely distant from the picture plane. In this type of projection, called parallel projection, there is no center of projection and the projecting rays (Figure 2.2) are parallel, there is no horizon line on which parallel lines converge at vanishing points, and parallel lines in the scene are depicted as parallel lines in the picture. It turns out that Perkins's laws are not just laws of perception: They also state the possible parallel projections of rectangular vertices. As we will see presently, Perkins's laws are not generally applicable to central projection. That is, certain geometrically correct central projections give rise to pictures that violate Perkins's laws and therefore do not look right.

Fig.7.14 Shape that is seen as a rectangular prism with mirror-symmetric, irregular, pentagonal cross section because it obeys an extension of Perkins's second law.		Fig.7.15 Figure that is not seen have regularity of Figure 7.14 because it does not obey extension of Perkins's laws.

Perkins's laws were independently discovered by Roger N. Shepard and Elizabeth Smith in an experiment⁴ that studied the perception of vertices of cubes, tetrahedrons (in which three edges meet at 60° angles), and plane patterns like the Mercedes-Benz equiangle trademark (in which three lines in a plane meet at 120° angles). Figure 7.16 shows the three objects studied. Shepard and Smith created 122 patterns, each of which was a circle with three radii (see Figure 7.17). The orientation of one of the radii was held fixed: It was always horizontal. Each pattern differed from others in the disposition of the other two radii; subjects were asked to say of each pattern whether it was an acceptable drawing of each of the three objects studied.

Fig.7.16 Three objects that participants in the Shepard and Smith experiment were asked to compare to drawings. Upper panel: Mercedes-Benz equiangle trademark (rotated 90°); middle panel: vertex of a cube; lower panel: vertex of a tetrahedron. The pictures of these objects all contain a "fork" (see Figure ), for which (roughly) f1 = f2 = 120°..		Fig.7.17 Shepard and Smith stimulus specifications. Upper right: If one radius, r1, is fixed, two angles can specify orientation of the other two radii. Q1, is measure of angle between r1 and r2; Q2 is measure of angle between r2 and r3. Lower left: Half the forms (remaining forms are mirror images of forms shown here) used in experiment. Forks are forms for which Q1 + Q2 > 180° tees are forms for which Q1 + Q2 = 180° arrows are forms for which Q1 + Q2 < 180° and ells are forms for which Q1 orQ2 = 180° (angles labeled 0° here are small angles, measuring roughly 7.5°, so as to ensure that there will always be three lines in each form)..

		Fig.7.18 Proportion of subjects accepting each pattern as representing Mercedes-Benz equiangle (panel A), vertex of cube (panel B), and vertex of tetrahedron (panel C). Areas of disks in three panels (whose organization parallels that in Figure 17) represent proportion of subjects accepting patterns as projections of three types of objects. Dashed boundaries in three panels delimit stimuli that are possible parallel projections of each type of object. In panel B, these boundaries also delimit stimuli that obey Perkins's laws.

Figure 7.18 shows the results of the experiment. The data of greatest interest to us are those shown in panel B: For all the stimuli that obeyed Perkins's laws, more than 50 percent of the subjects accepted the pattern as the representation of the vertex of a cube; for all the stimuli that violated Perkins's laws, almost no subjects accepted the pattern as a representation of the vertex of a cube.

Let us recapitulate: A perceiver is faced with the dilemma of perspective when a picture drawn in perspective is seen from a vantage point other than the center of projection.

The perceiver must either assume that the center of projection coincides with the perceiver's vantage point, in which case the proper interpretation of the scene will change with each change of vantage point, or the perceiver must infer the location of the center of projection and reconstruct the proper scene as it would be seen from that point. Because we have seen that perspective is robust in the face of changing vantage points, the latter must be the case. Furthermore, because inferring the location of the center of projection seems to require an assumption that the objects represented are rectangular, we examined the question of the perception of rectangularity of corners in pictures. We discussed two possibilities: that the perception of rectangularity is based on familiarity with the sorts of objects represented and that rectangularity is based on geometric rules that apply to the configuration of line junctures that represent right-angled vertices. We concluded in favor of the latter.