"Opticality" in early Renaissance painting:
Smoke... or mirrors?

van Eyck's "Portrait of Cardinal Niccolò Albergati": Alternate non-optical explanations

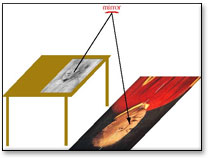A plausible schematic of the Hockney/Falco setup shows the silverpoint on a small table, a concave mirror and the projected image on the canvas 40% farther away (as required by the magnification).

We first consider images Hockney and Falco enlist in support of their theory: two portraits of Cardinal Niccolò Albergati by van Eyck. The earlier is a silverpoint (1431), the latter an oil about 40% larger, executed the following year. Upon expanding the silverpoint image by 40% and aligning the images, their correspondence is indeed striking. It leads Hockney and Falco to propose that van Eyck used an epidiascope -- a primitive "opaque projector" -- to copy and enlarge the silverpoint image for the oil version.

First, as remarked by Bernhard Sharratt in his review of Secret Knowledge, the correspondence between the images, while close, is not "almost perfect," as claimed by Hockney and Falco (even for the individual patches that match quite well). Nevertheless, let us accept that the match is excellent.

Falco demonstrates that there are three "exposures," so to speak -- three image patches for which the correspondence is quite good. The first patch consists of the mouth, nose and much of his face at the left. If the painting is then shifted to the right (by 36 pixel-block steps in my electronic images, or about 4mm on the silverpoint), then the earlobes and collars match well. If the painting is then shifted up by 18 pixel-block steps, the pinna (top of ear) matches well. These shifts -- and the Hockney/Falco explanation for them and my alternative -- will be important in the analysis below.

1. Two random bumps		2. One "lucky" horizontal bump		3. Two "lucky" bumps (one horizontal, one vertical)

Hockney and Falco write: "The painted portrait, created the following year, was 40% larger than the drawing, and yet -- observe -- when recast at the same size, matches it almost perfectly. How else to account for the convergence except by way of some sort of optical projection?"

"How else"? Three techniques immediately spring to mind: "eyeballing," grid constructions, and pantographs.

Consider the first technique for duplicating the Albergati portrait: eyeballing. Given the fidelity with which some modern representational artists can copy from nature or from other paintings without optical aids, it is not unreasonable to entertain the notion that the oil painting was "eyeballed" (in Mr. Hockney's term). I've seen many students in the National Gallery and elsewhere copying masterpieces with great fidelity. We must not forget that that in the case of the Albergati portrait, the copier would be the same artist as that for the original, and hence more likely to give an accurate copy. At the very least, such eyeballing does not rely on technology that never appears in the historical record (see below).

Now consider the second technique for duplicating the Albergati silverpoint (and the one I favor): grid constructions. In the grid method, a rectangular grid is drawn over the original silverpoint or constructed from threads held taught across its surface so as not to mark the original (but see below).

Grid construction for the enlargement of the Albergati portrait.

I made my own 40% enlargement of the Albergati portrait by this method using merely a ruler and T-square, as shown. I then scanned my enlargement, reduced it by 40% and overlapped it with the original image. The overlap and match is excellent -- even better than in the case remarked upon by Hockney and Falco. Admittedly, the subtle quality of line (e.g., variation in thickness) is missing due to my limited artistic abilities, but even in the Hockeny/Falco method the quality of line depends upon the artist, not upon the projection method. Incidentally, I left the rectangular grid on my enlargement, though clearly I could have erased it; regardless, if the enlargement were the basis for an oil painting, the oil paint would obscure the grid.

When the enlarged drawing is electronically reduced and aligned to overlap the original silverpoint, the correspondence is excellent.

The explanation by grid construction explains numerous aspects of these images that the Hockney/Falco theory does not. Consider the relative shifts in alignments between the silverpoint and scaled painting. Hockney and Falco suggest that van Eyck "bumped" one of the artworks during the copying in an epidiascope. If indeed van Eyck used an epidiascope this explanation of the origin of the shifts seems eminently plausible. Nevertheless on closer inspection the explanation fails.

You can see this by performing the following extremely simple experiment. Place a notebook or paperback book on a flat tabletop -- this will represent one of van Eyck's image surfaces (paper or canvas). Now randomly "bump" the notebook. Now randomly "bump" it again in another direction. Unless you planned otherwise, the book became rotated just a bit in the process. In fact, there is no detectable rotation for the image patches in the van Eyck image pairs. More importantly, it is highly unlikely that your any of your bumps moved the notebook exactly horizontally or vertically .

Shifts, either in your simple bumping experiment or in van Eyck's studio. We can choose any alignment as our base or origin (red dot), and can draw a circle through the most distant overall shift (green dot). We indicate the third shifted position with a blue dot.

The first diagram illustrates random bumps, as we might expect in the Hockney/Falco theory since there is no compelling preference for horizontal or vertical bumps. The second illustrates one "lucky" horizontal bump. The third illustrates two "lucky" bumps -- one horizontal and one vertical -- and would be extremely unlikely in the Albergati portraits according to the Hockney/Falco theory. In fact, though, the right diagram shows the actual shifts, measured in units of pixel-blocks in Adobe Photoshop, where M corresponds to the mouth patch in alignment, the L to the earlobe patch in alighnment and the P to the pinna patch.

The horizontal and vertical shifts are easily explained in the grid construction: van Eyck miscounted the grid square in the horizontal or vertical directions or for artistic reasons wanted to resize the head slightly while still employing the grid. The grid explanation goes further: it explains the relative distances of the shifts. If van Eyck miscounted by one grid square in the vertical direction and two grid squares in the horizontal direction, then the ratio of these distances would be 1:2, just as we find (18:36).

But the grid construct explains even more. Go back and expand the image of the silverpoint and notice the two vertical lines running the full height of the work. (A dim third vertical line between them, running partway down the image, as well as a very dim region of square grids at the left are visible too.) These are just the lines that are required by the grid construction method, and their separation corresponds to the relative shift (36 pixel-blocks) that we found above. I'm seeking an infra-red image of the oil painting to reveal any underdrawing, and will post the image here as soon as it becomes available.

A pantograph. These mechanical tracing devices (German: Storchenschnabel, or "stork's beak"!) have been used for copying images and paintings for centuries.

Finally, consider the third method for duplicating the Albergati portrait: pantographs. Leonardo used one. They are based on simple principle of the parallelogram in Euclidean geometry understood twenty-three centuries ago. The artist moves a pointer attached to one part of the pantograph along the outline of the original flat image, and a pencil attached to another part traces out the image but at a larger scale. The placement of the pointer and pencil determines the overall scale, and can even be set to shrink the image. The devices are quite simple, as shown at the left; as a child I made pantograph from a toy metal erector set.

Pantographice seu ars delineandi Christoph Scheiner, 1631 Two uses of pantographs are shown in this engraving. The cloudlike artist in the middle looks through a stationary peephole (to ensure consistent viewpoint) and moves a pointer hanging off the edge of the canvas so as to intercept the sightline to the bust being drawn.

the pantograph at right, linked to a pointer by bars and axles, then becomes aligned with the corresponding point on the canvas, which the artist then marks. In this way, the pantograph is used to draw the three-dimensional bust.

The putto at the lower right is tracing a small flat picture on the table and the attached pantograph moves a pencil and thereby draws the image at a larger scale. Although we don't have records of the use of such a device by van Eyck, this simple device was used by Leonardo a few decades later to copy and scale some of his images.

Before we leave the Albergati portrait, we should consider the suggestion made in passing by Mr. Hockney: that the small pupils in the portrait indicate the sitter was under intense illumination, presumably sunlight, as required by the Hockney/Falco projection method. Indeed, small pupils are consistent with bright illumination, but there are other explanations. Small pupils arise frequently in the elderly for a number of other, biological reasons. If they are due to bright illumination, though, we can only wonder why such small pupils do not appear in other Renaissance portraits purportedly made under bright illumination required by the Hockney/Falco method.

Summary: The explanation through grid constructions is principled, parsimonious and elegant. It explains numerous facts -- such as why the shifts between patches are horizontal and vertical and their distances are the simple ratio 1:2. According to the Hockney/Falco all these facts are highly unlikely; other facts are not even considered such as two vertical rule lines in the silverpoint, and their mutual separation. Modern simple reenactments support the grid construction explanation while no such reenactments have been done for the Hockney/Falco theory. Finally, the grid construction relies on technology clearly available to van Eyck while the Hockney/Falco explanation relies at its very core upon what would have been the most sophisticated optical instrument of its day, for which there are myriad technical problems and for which we have no corroborating textual evidence (see below).